🏰 Palace Window

Search

SearchSearch

Heaps & Queues

Heaps & queues are data structures whose characteristics lend themselves to efficient solutions of certain problems. E.g. heaps allow logn insertion & deletion of elements in order. This can allow its user to avoid searching a list n times & allow an nlogn solution instead of an n^2 one.

 

Heapify

How can a size N tree, usually passed in as an array, be rearranged in O(n) so that its nodes all satisfy the heap property, i.e. every node in the tree has a value >= (max heap) or <= (min heap) than its children.

Algorithm

heapify-algorithm.png

Python Implementation

def maxHeapify(A, i):
    left = 2 * i + 1
    right = 2 * i + 2
    largest = i
    if left < len(A) and A[left] > A[largest]:
        largest = left
    if right < len(A) and A[right] > A[largest]:
        largest = right
    if largest != i:
        A[i], A[largest] = A[largest], A[i]
        A = maxHeapify(A, largest)
    return A
 
 
def buildMaxHeap(A):
    for i in range(len(A) // 2, -1, -1):
        A = maxHeapify(A, i)
    return A

Complexity

The cost of a call to maxHeapify is O(h), a node may have to swap from its height, h times, to a leaf. The last level on a binary tree has at most n/2 nodes & makes 0 calls to maxHeapify, the next level has n/2^2 nodes & makes at most n/2^2 calls to max heapify. As we approach the height of the root node, h increases. 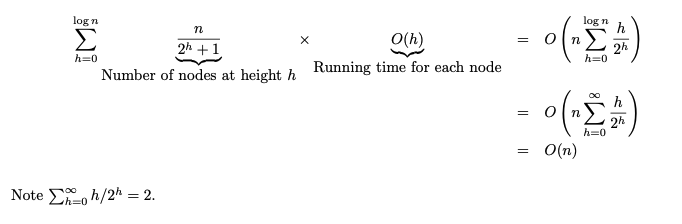If we sum over the calls to # of maxHeapify calls * O(h) of each call, we have the following: heapify-complexity.png

 

Last Stone Weight

Given an array of integers representing the weights of stones, smash the two heaviest stones together repeatedly until one or no stones remain. If a stone is heavier it survives the smashing with a new weight less the weight of the lighter stone. Stones equal in weight are both destroyed when smashed together.

Explore

  1. Use a heap (logk insert/retrieve) to store the stone weights.
  2. Keep popping the heaviest two stones & smashing them, inserting any left over stone.
  3. When 1 or no stones remain, return the weight of them. Note: Using a second heap could speed things up in practice but not in theory.

Python Solution

from heapq import heappush, heappop, heapify
 
 
class Solution:
    def last_stone_weight(self, S) -> int:
        N = len(S)
        # heapify in place is O(n) < N insertions
        # python heap implementation is a min heap -> use negatives
        for i in range(N):
            S[i] = -S[i]
        heapify(S)
 
        while len(S) > 1:
            a = -heappop(S)
            b = -heappop(S)
            if a != b:
                heappush(S, -(max(a, b) - min(a, b)))
 
        if len(S) == 0:
            return 0
 
        return -S[0]

Complexity

We construct a size N heapq in place, Heapify, in N time & pop its top two items repeatedly in constant time, pushing at most one item back into the heap each time for a max n-1 iterations. Each insertion into the heap is logn, therefore, we have an O(nlogn) time & O(n) space solution.

Graph View